ごめんなさい…、長くなってしまいました…。

　・荷重などの外力に対して部材内部に生じる抵抗力のこと

　・任意の点において左右（上下）の力は「必ず」つりあう

　・↑任意の点の応力を求める場合にはいずれか片方（右or左）を見ればOK

　左右の力は「等しい大きさ」の「方向が逆」でつりあう

　　　↑何の事やら…、分かりませんね。ちょっとヤヤコシイので以下の例で説明します。

　例1　1本の棒の一端に圧縮の力がかかっている場合

(1)棒の左端（A点）に力「P」を加えます。

　　　　　 　　A点に荷重P（右）がかかっています

(2)棒が動かない為には反対側のB点で支えなければなりません。

　　　　　 　　PとP'は大きさ同じ・方向逆

　この状態で「安定」です。部材は「圧縮」されています。

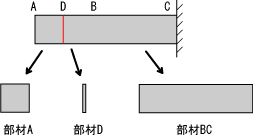
(3)部材の内部を見てみます。C点を切断面として部材を3つに分割します。

　　　

(4)棒全体が圧縮されているので部材Cも圧縮されています。



(5)上の図はちょっとオカシイです。このままでは部材A・Bが動いてしまいます。

部材A・Bともに元々圧縮されていたので以下の様になります。



(6)上図を良く見ると全ての部材ともに左右の力がつりあっています。

力1＝力2、力3＝力4、力5＝力6、また全体として力1＝力6

　C点は何処に移動しても上記関係は変化しません。したがって、今回の例では部材のどこを切ったとしても等しい圧縮力Pがかかっていることになります。





では次です。実際の建築士の問題に近づけて（無理やり…）みます。

　例2　1本の棒の2ヶ所に圧縮の力がかかっている場合

(1)棒のA点に2P、B点にPの右向きの力がかかっています。

(2)C点が壁になっているとすると、反力（支える力）が生じます。



(3)D点で切断してみます。

　　

(4)部材Aに注目し、左端の2Pの力とのつりあいを確認してみます。



(5)部材Aの右端の2P（青矢印）と部材Dの左端（赤矢印）はつりあい、さらに部材Dの左端（赤矢印）は部材Dの右端（緑矢印）とつりあいます。



(6)さて、ここからが問題です。部材Dの右端の2P（緑矢印）と部材BCの左端（黄矢印）はつりあわなければなりません。…が、部材BCの右端には反力3P（紫矢印）があります。結局は部材BC中には荷重P（黒矢印）があるので、以下の様になります。



(7)ヤヤコシクなってきましたが、今行っていることは切断面Dにおける応力を求めることです。上図より部材Dは2Pの圧縮を受けています。切断面はA-B間のどこをとっても同じ2P圧縮になります。しかし、荷重のかかっているB点を超えてしまうと以下の様に3Pの圧縮をうけます。



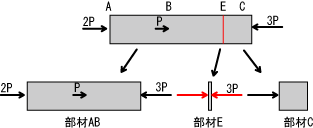
(8)まとめてみましょう。薄赤の部分が2P圧縮、薄青の部分が3Pの圧縮です。



(9)上図が実は最も重要です。材料の端、荷重のかかっている所、支点、接点で応力は変化します。実際の問題では以上の点で部材を分けて考える必要があります。また、部材の左右の力は「必ず」つりあいますので計算する際にはどちらか片方の力のみをリストアップすれば応力計算可能です（って事は、試験の際には反対側の力も計算して計算ミスの確認も出来ますね）。

(10)例題は軸方向力で解説しましたが、「せん断力」「曲げモーメント」でも同じです。